LeetCode笔记

Serendy Magician

2025-12-02 13:37:19 2025-12-02 13:37:19 创建 2025-12-11 20:42:53 2025-12-11 20:42:53 更新

面包追求科技研讨间

Note

18.2k 字 73 分钟

Python数据结构

0. 总体地图：都有哪些东西？

按大类分一下：

序列（Sequence）
list, tuple, str, range
映射（Mapping）
dict
集合（Set）
set, frozenset
常用高级容器（collections / 标准库里的）
deque, defaultdict, Counter, namedtuple
以及 heapq 堆

你 90% 的代码和刷题基本被这几位承包。

1. list：动态数组（Python 亲儿子）

本质：动态数组，支持下标访问，可变，有序。

1.1 创建

a = []               # 空列表
a = [1, 2, 3]
a = list(range(5))   # [0,1,2,3,4]
a = [0] * 10         # 长度为 10 的全 0 列表

1.2 访问 & 切片

a[i]          # 下标访问
a[-1]         # 最后一个
a[1:4]        # 切片 [1,2,3]
a[::-1]       # 反转视图

1.3 修改

a[i] = 10
a.append(x)        # 末尾加元素，O(1) 均摊
a.extend([4, 5])   # 连接列表
a.insert(2, x)     # 在下标 2 插入，O(n)

1.4 删除

a.pop()       # 弹出末尾，O(1)
a.pop(i)      # 弹出指定位置，O(n)
del a[i]
a.remove(x)   # 删第一个等于 x 的元素，O(n)
a.clear()     # 清空

1.5 其他常用

len(a)
x in a
a.index(x)
a.count(x)
a.sort()                # 原地排序
b = sorted(a)           # 返回新列表

记忆关键：随机访问 O(1)，中间插删 O(n)，末尾 append/pop O(1)。

2. tuple：不可变的“只读 list”

本质：有序、不可变，支持下标访问，可以当字典 / 集合的 key。

2.1 创建

1
2
3

t = (1, 2, 3)
t = 1, 2, 3           # 省略括号也行
t = tuple([1, 2, 3])

2.2 用途

作为字典 key：mp[(x, y)] = value
存状态：state = (i, mask)
函数多返回值：return x, y

操作类似 list（访问、切片），就是不能改。

3. str：不可变字符串

本质：字符序列，不可变，也可以当 dict/set 的 key。

3.1 常用操作

s = "hello"

s[0]        # 'h'
s[-1]       # 'o'
s[1:4]      # 'ell'
len(s)

s.upper()
s.lower()
s.strip()
s.split(',')    # 分割
','.join(list)  # 拼接

s.replace('a', 'b')

典型刷题用途：

当哈希 key，比如：key = ''.join(sorted(s))

字符串处理、前缀/后缀判断

4. dict：哈希表（键值映射）

本质：哈希表，支持平均 O(1) 的插入、删除、查询。

4.1 创建

1
2
3

mp = {}
mp = dict()
mp = {'a': 1, 'b': 2}

4.2 插入 / 修改

1 2	mp['a'] = 1 mp['a'] = 2 # 覆盖

4.3 访问

1
2
3

v = mp['a']                  # 不存在会 KeyError
v = mp.get('a')              # 不存在返回 None
v = mp.get('a', 0)           # 不存在返回默认值 0

4.4 遍历

for k in mp:                 # 遍历 key
    ...

for k, v in mp.items():      # key, value
    ...

for v in mp.values():        # 只要 value
    ...

4.5 删除

1
2
3

del mp['a']
mp.pop('a', None)            # 不存在也不报错
mp.clear()

记忆关键：

key 必须可哈希：int, str, tuple 等

查询 / 插入 / 删除平均 O(1)

5. set：去重 + 成员判断神器

本质：只存 key 的哈希表，无序，元素唯一。

5.1 创建

1
2
3

s = set()
s = {1, 2, 3}
s = set([1, 2, 2, 3])    # 自动去重

5.2 常用操作

s.add(4)
s.remove(2)        # 不存在会报错
s.discard(2)       # 不存在就算了，不报错
s.clear()

3 in s             # 成员判断 O(1)
len(s)

5.3 集合运算

a | b      # 并集
a & b      # 交集
a - b      # 差集
a ^ b      # 对称差

常见用途：判重、visited 集合、求交并差。

6. collections 里常见几位

6.1 `deque`：双端队列

from collections import deque

q = deque()
q.append(1)        # 右端入
q.appendleft(2)    # 左端入
q.pop()            # 右端出
q.popleft()        # 左端出

特点：

头尾插删 O(1)
适合队列、双端队列、BFS、滑动窗口等

6.2 `defaultdict`：带默认值的 dict

from collections import defaultdict

mp = defaultdict(list)
mp['a'].append(1)
mp['a'].append(2)

mp2 = defaultdict(int)
mp2['x'] += 1

特点：

访问不存在的 key 时自动创建默认值，省去了 if 判断
常用于：分组、计数

6.3 `Counter`：频数统计

from collections import Counter

cnt = Counter([1, 2, 2, 3])
cnt[2]          # 2
cnt.most_common(2)  # [(2, 2), (1, 1)]  频率 Top 2

用途：

字符 / 数字频次统计
Top K 高频元素
判断两个串是否字符构成相同

6.4 `namedtuple`：轻量级“结构体”

from collections import namedtuple

Point = namedtuple('Point', ['x', 'y'])
p = Point(3, 4)
p.x, p.y

用途：

含义更清晰的“元组”，提高可读性

7. heapq：最小堆（优先队列）

heapq 不是一个类型，而是一堆操作函数，把 list 当堆用。

import heapq

h = []
heapq.heappush(h, 3)
heapq.heappush(h, 1)
heapq.heappush(h, 5)

x = heapq.heappop(h)   # 1，最小的先出来

特点：

Python 默认是小根堆
操作复杂度：push/pop O(log n)
常见用途：
- 维护前 K 小 / 大（配合取负数）
- 合并区间、调度、最短路（Dijkstra）

8. 一个简单小总表（当速查用）

类型	底层	典型操作 & 复杂度
`list`	动态数组	随机访问 O(1)，末尾增删 O(1)，中间 O(n)
`tuple`	动态数组(只读)	访问 O(1)，可哈希，可做 key
`str`	数组(只读)	访问 O(1)，可哈希，常作 key
`dict`	哈希表	查/增/删平均 O(1)
`set`	哈希表	查/增/删平均 O(1)
`deque`	双端队列	头尾增删 O(1)
`Counter`	基于 dict	统计频次 O(n)
`defaultdict`	基于 dict	自动初始化 value
`heapq`	二叉堆	push/pop O(log n)

哈希表

直接“算出”对象位置：散列

散列查找法的两项基本工作： ①计算位置：构造散列函数确定关键词存储位置； ② 解决冲突：应用某种策略解决多个关键词位置相同的问题

时间复杂度几乎是常量：O（1），即查找时间与问题规模无关！

“散列（Hashing）” 的基本思想是：

（1）以关键字key为自变量，通过一个确定的函数 h（散列函数），计算出对应的函数值h(key)，作为数据对象的存储地址。

（2）可能不同的关键字会映射到同一个散列地址上，即h(keyi ) = h(keyj )（当keyi ≠keyj），称为“冲突(Collision)”。 —-需要某种冲突解决策略

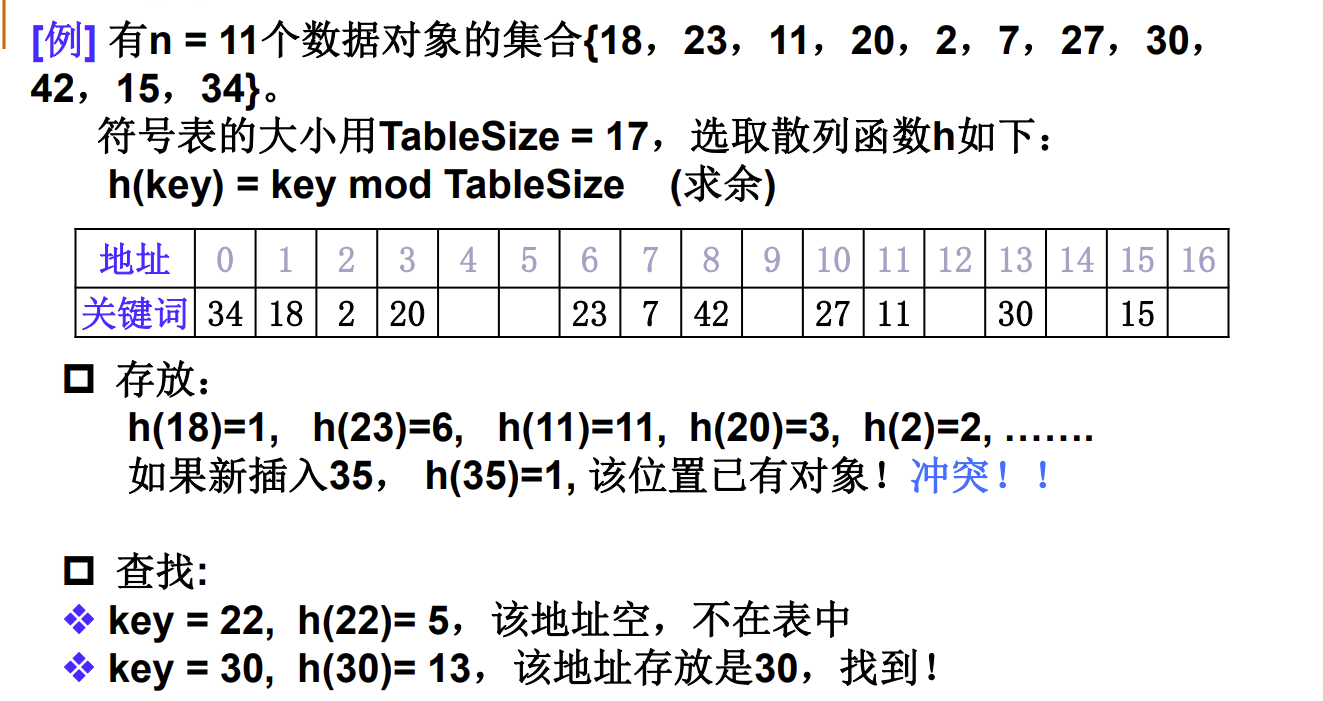
装填因子（Loading Factor）：设散列表空间大小为m，填入表中元素个数是n，则称α＝ n / m为散列表的装填因子

α＝11 / 17 ≈ 0.65。

散列（哈希）函数的构造方法

计算哈希函数所需时间关键字的长度哈希表的大小关键字的分布情况记录的查找频率

1 直接定址法

取关键词的某个线性函数值为散列地址，即 h(key) = a × key + b (a、b为常数)

2 除留余数法

散列函数为：h(key) = key mod p（p是素数）

3 数字分析法

如果可能出现的关键字的数位相同，且取值事先知道，则可对关键字进行分析，取其中“分布均匀”的若干位或它们的组合作为哈希表的地址。

分析数字关键字在各位上的变化情况，取比较随机的位作为散列地址

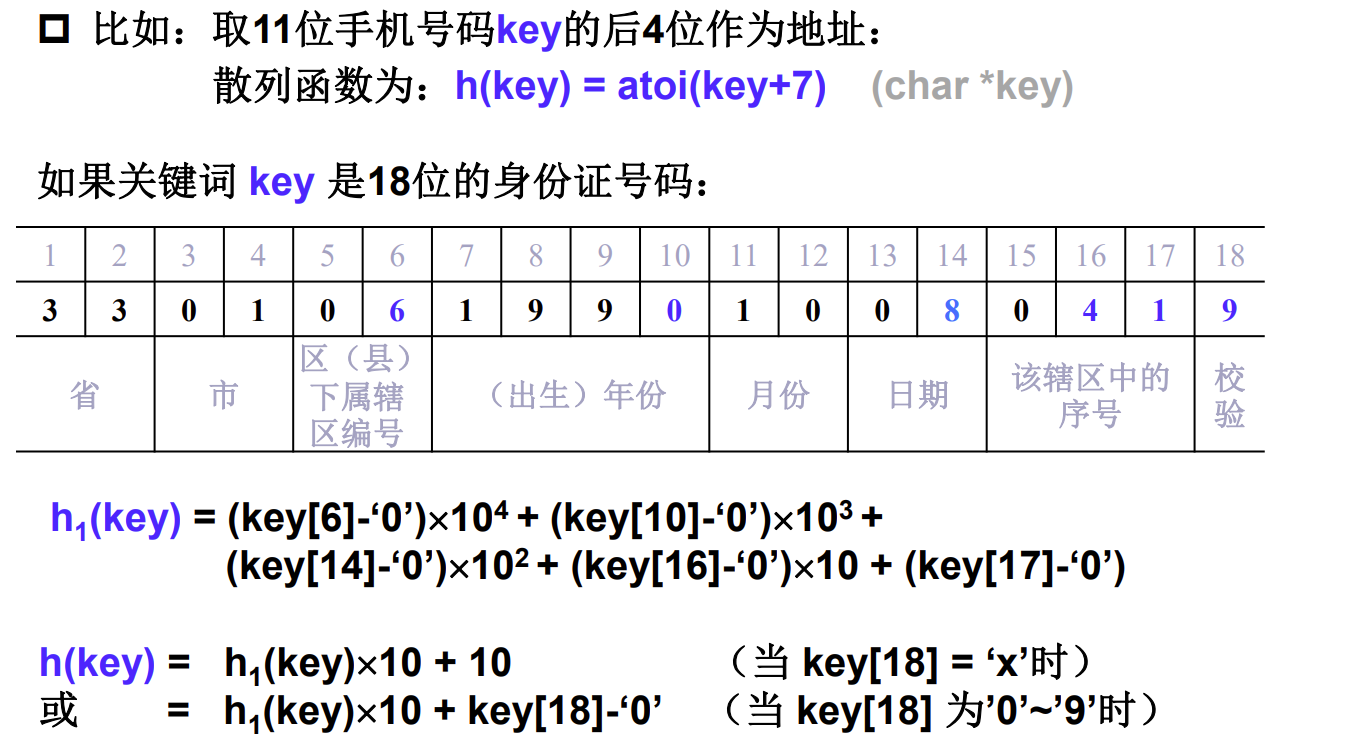
4 折叠法

若关键字的位数很多，且每一位上数字分布大致均匀，则可采用移位叠加或间界叠加，即将关键字分成若干部分，然后以它们的叠加和(舍去进位) 作为哈希地址。移位叠加是将分割后的每一部分的最低位对齐，然后相加；间界叠加是从一端向另一端沿分割界来回折叠，然后对齐相加。

5 平方取中法

如果关键字的所有各位分布都不均匀，则可取关键字的平方值的中间若干位作为哈希表的地址。由于一个数的平方值的中间几位数受该数所有位影响，将使随机分布的关键字得到的哈希函数值也随机。

6 随机数法

当关键字不等长时，可取关键字的某个伪随机函数值作为哈希地址。

Hash(key) = random(key)

冲突处理方法

常用处理冲突的思路： ① 换个位置: 开放地址法 ② 同一位置的冲突对象组织在一起: 链地址法

1 开放定址法

一旦产生了冲突（该地址已有其它元素），就按某种规则去寻找另一空地址

若发生了第 i 次冲突，试探的下一个地址将增加di，基本公式是： hi (key) = (h(key)+di ) mod TableSize ( 1≤ i < TableSize )

di 决定了不同的解决冲突方案：线性探测、平方探测、双散列。

1 线性探测法 P130

线性探测法：以增量序列 1，2，……，（TableSize -1）循环试探下一个存储地址。

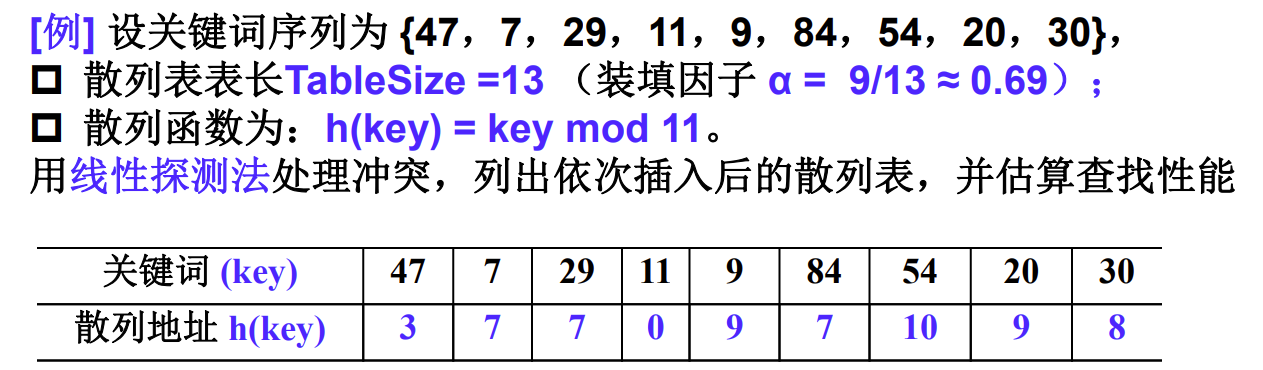
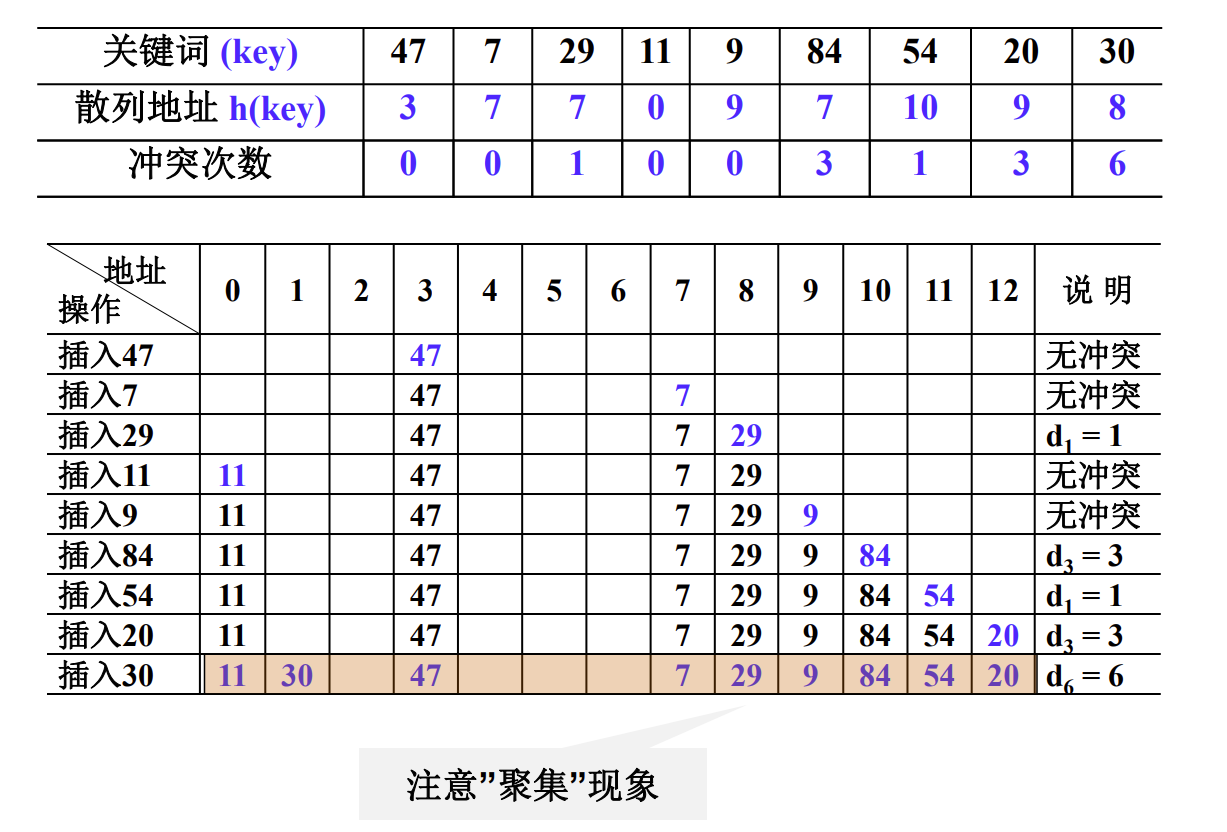
2 平方探测法 P132

平方探测法：以增量序列1^2^ ，-1^2^ ，2^2^ ，-2^2^ ，……，q^2^ ，-q^2^ 且q ≤ [TableSize/2] 循环试探下一个存储地址。

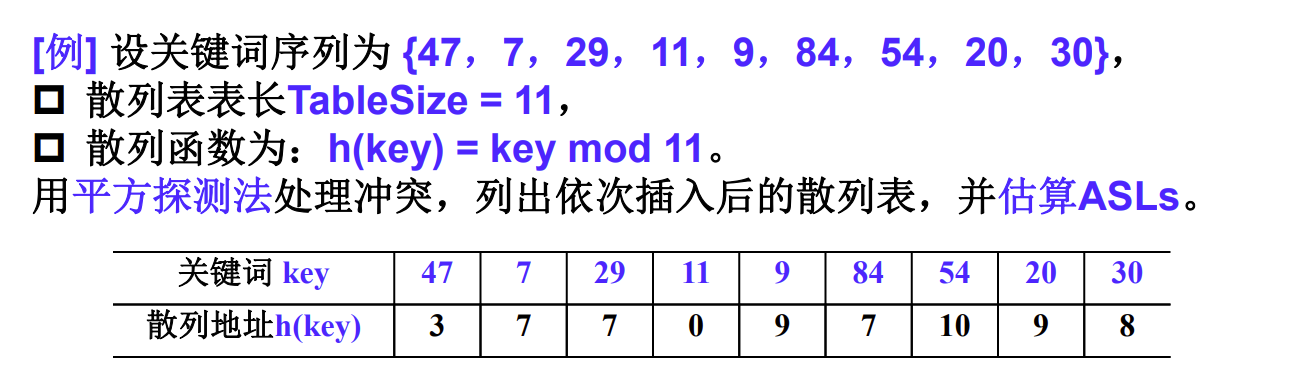
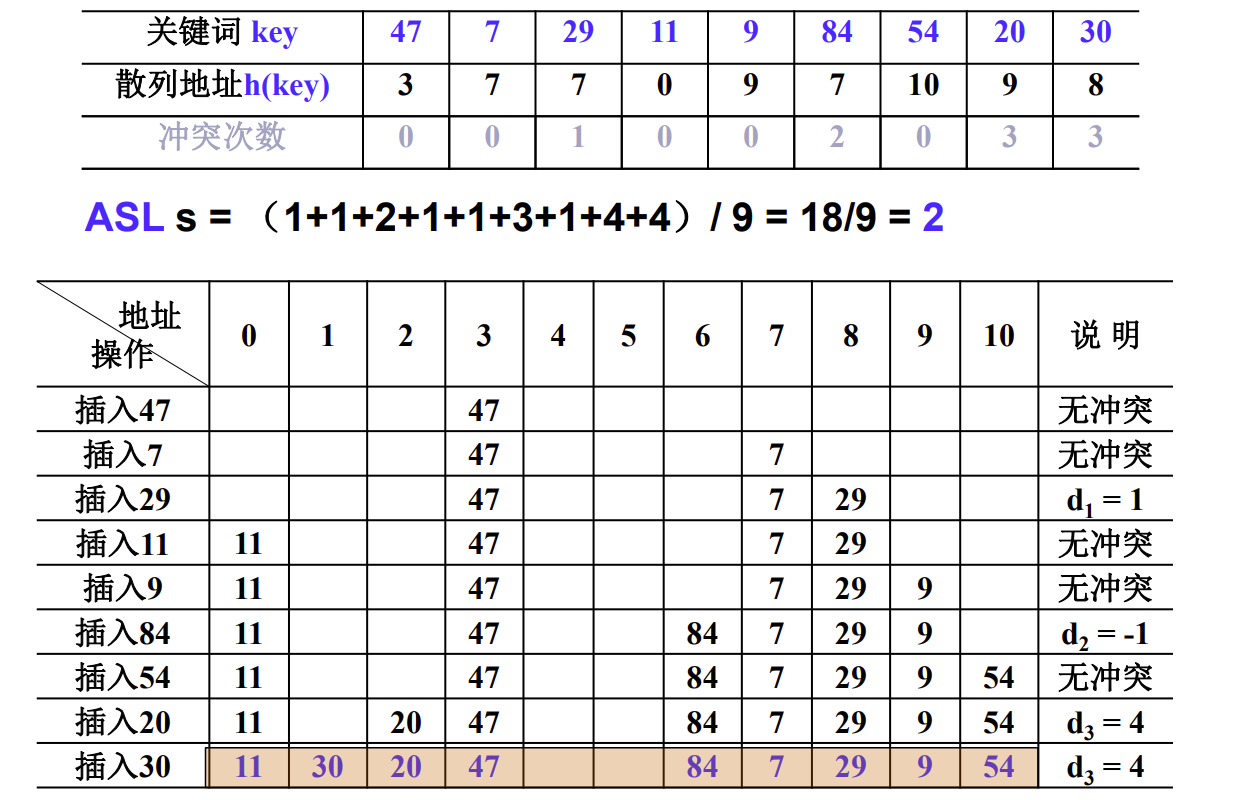
3 双散列探测法 P133

双散列探测法: di 为i*h2 (key)，h2 (key)是另一个散列函数探测序列成：h2 (key)，2h2 (key)，3h2 (key)，……

对任意的key，h2 (key) ≠ 0 ！

探测序列还应该保证所有的散列存储单元都应该能够被探测到。选择以下形式有良好的效果： h2 (key) = p - (key mod p) 其中：p < TableSize，p、TableSize都是素数。

2 再哈希法

Hi =RHi (key) i=1,2,…,h RHi 均是不同的哈希函数，即在同义词产生地址冲突时计算另一个哈希函数地址，直到冲突不再发生，这种方法不易产生“聚集” ，但增加了计算的时间。

3 链地址法

将所有关键字为“同义词”的记录链接在一个线性链表中。此时的哈希表以 “指针数组”的形式出现，数组内各个分量存储相应哈希地址的链表的头指针。

4 建立一个公共溢出区

设立一个基本表HashTable[0..m-1]和一个溢出表OverTable[0..v]，所有关键字和基本表中关键字为同义词的记录，一旦冲突，都填入溢出表。

算法实现

结构声明

typedef struct
        HashTbl *HashTable;
struct HashTbl {
    int TableSize;
    Cell *TheCells;
} H;

初始化哈希表

HashTable InitializeTable(int TableSize) {
    HashTable H;
    int i;
    if (TableSize < MinTableSize) {
        Error("散列表太小");
        return NULL;
    }
    /* 分配散列表 */
    H = (HashTable) malloc(sizeof(struct HashTbl));
    if (H == NULL)
        FatalError("空间溢出!!!");
    H->TableSize = NextPrime(TableSize);
    /* 分配散列表 Cells */
    H->TheCells = (Cell *) malloc(sizeof(Cell) * H->TableSize);
    if (H->TheCells == NULL)
        FatalError("空间溢出!!!");
    for (i = 0; i < H->TableSize; i++)
        H->TheCells[i].Info = Empty;
    return H;
}

平方探测法

Position Find(ElementType Key, HashTable H) /*平方探测*/{
    Position CurrentPos, NewPos;
    int CNum; /* 记录冲突次数 */
    CNum = 0;
    NewPos = CurrentPos = Hash(Key, H->TableSize);
    while (H->TheCells[NewPos].Info != Empty &&
           H->TheCells[NewPos].Element != Key) {
        /* 字符串类型的关键词需要 strcmp 函数!! */
        if (++CNum % 2) { /* 判断冲突的奇偶次 */
            NewPos = CurrentPos + (CNum + 1) / 2 * (CNum + 1) / 2;
            while (NewPos >= H->TableSize)
                NewPos -= H->TableSize;
        } else {
            NewPos = CurrentPos - CNum / 2 * CNum / 2;
            while (NewPos < 0)
                NewPos += H->TableSize;
        }
    }
    return NewPos;
}

插入操作

void Insert(ElementType Key, HashTable H) { /* 插入操作 */
    Position Pos;
    Pos = Find(Key, H);
    if (H->TheCells[Pos].Info != Legitimate) {
        /* 确认在此插入 */
        H->TheCells[Pos].Info = Legitimate;
        H->TheCells[Pos].Element = Key;
        /*字符串类型的关键词需要 strcpy 函数!! */
    }
}

性能分析

一般情况下，在哈希函数为“均匀”的前提下，哈希表的平均查找长度仅取决于处理冲突的方法和哈希表的装填因子α。

🎯 两数之和（Two Sum）

做题次数	做题时间	做题结果
第一次	2025.12.01	掌握一遍哈希法，用空间换时间，写出 O(n) 解法 ✅

🧩 题目描述

给定一个整数数组 nums 和一个整数目标值 target，请你在数组中找到两个元素，使得：

1	nums[i] + nums[j] == target` 且 `i != j

返回这两个元素的下标 [i, j]，顺序无所谓。

额外条件：

每种输入只会对应一个答案
不能重复使用同一个元素（也就是不能拿自己加自己，除非数组里有两个相同值）

📌 示例

示例 1

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：nums[0] + nums[1] = 2 + 7 = 9

示例 2

输入：nums = [3,2,4], target = 6
输出：[1,2]
解释：nums[1] + nums[2] = 2 + 4 = 6

示例 3

输入：nums = [3,3], target = 6
输出：[0,1]
解释：用的是两个不同位置的 3，不是同一个元素用两次。

🧠 解题思路：哈希表，边走边找对象

最原始暴力思路：双层循环枚举所有 (i, j)，看 nums[i] + nums[j] == target，复杂度 O(n^2)，面试官会礼貌微笑然后把你挂了。

更聪明点的做法：一遍扫描 + 哈希表，核心想法是：

当前数是 x，我需要找的是 target - x，所以问题变成： “我之前有没有见过一个数，刚好是 target - x？”

具体过程：

准备一个哈希表 mp：
- key：数组中的值
- value：这个值出现的下标
遍历数组，枚举当前下标 i 和当前值 nums[i] = x：
- 计算“理想对象”：need = target - x
- 查看哈希表里有没有 need
  - 如果有：[mp[need], i] 就是一对答案，直接返回
  - 如果没有：把当前值记下来 mp[x] = i
因为题目保证一定有解，所以遍历过程中必然能提前 return。

逻辑顺序是：不是“先存自己，再找对象”，而是先看看能不能跟别人凑一对，不行再登记信息。

✅ Python 代码（哈希一遍扫描）

from typing import List

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        # 哈希表：值 -> 下标
        mp = {}

        for i, x in enumerate(nums):
            need = target - x
            if need in mp:
                # 找到了之前的互补值
                return [mp[need], i]
            # 没找到就把当前值记下来
            mp[x] = i
        
        # 理论上不会走到这里，因为题目说一定有解
        return []

🧩 核心逻辑表

遍历数组时，对每个元素 x = nums[i]：

步骤	操作	说明
计算	`need = target - x`	需要一个“互补值”
查询哈希	`need in mp`?	之前是否出现过这个互补值
如果存在	返回 `[mp[need], i]`	之前那个下标 + 当前下标就是答案
如果不存在	`mp[x] = i`	把当前值登记，以便后面的数来匹配

思维模式：“我能不能和前面某个人凑 target？” 不能，就把自己信息写进“相亲表”，等后面的来找你。

⏳ 复杂度分析

时间复杂度：O(n) 每个元素只被访问一次，哈希表查询和插入都是平均 O(1)。
空间复杂度：O(n) 最坏情况下所有元素都被放入哈希表中。

🪄 小结口诀

两数之和常客题，
暴力双层别再提。

一遍扫描建字典，
目标差值先看清。

先查后存不乱用，
配对成功直接停。

✅ 关键词记忆：哈希表、互补值 = target - x、一遍扫描、先查后存

这题属于「八股基础款」，你现在写熟了，以后面试一上来看到它，就可以在心里说一句：谢天谢地，送分题。

🔤 字母异位词分组（Group Anagrams）

做题次数	做题时间	做题结果
第一次	2025.12.01	掌握“排序当签名 / 频次数组当签名”的哈希分组思路 ✅

🧩 题目描述

给你一个字符串数组 strs，请你把其中的字母异位词分到一组里，返回所有分组结果。

字母异位词：由相同字母构成，只是顺序不同，比如 "eat", "tea", "ate"。
返回的分组顺序随意，组内字符串顺序也随意，评测只看“分组是否正确”。

📌 示例

示例 1

输入：

1	strs = ["eat", "tea", "tan", "ate", "nat", "bat"]

输出（顺序可以不一样）：

1	[["bat"], ["nat","tan"], ["ate","eat","tea"]]

解释：

"bat"：孤家寡人一组
"nat" / "tan"：同一组
"ate" / "eat" / "tea"：同一组

示例 2

1 2	输入：[""] 输出：[[""]]

示例 3

1 2	输入：["a"] 输出：[["a"]]

🧠 解题思路：给每个单词“做指纹”，用哈希表分组

题目本质：

把“可以相互打乱重排得到的字符串”分到同一组。

很像这样一句话：

“你们长得不一样，但骨骼（字母构成）一样，就去同一个班。”

那我们要做的就是： 给每个字符串找一个“唯一代表它字母构成的标识”，作为哈希表的 key。

思路一：排序当“签名”（最常用、好写）

对每个字符串 s：

把字符排序：sorted(s)
排完后转成字符串，比如 "eat" → "aet"，"tea" → "aet"
这俩排序结果一样，就说明它们是异位词。

做一个哈希表：

key：排序后的结果，比如 "aet"
value：所有排序后是 "aet" 的原字符串列表

伪代码逻辑：

map = {}
for s in strs:
    key = ''.join(sorted(s))
    map[key].append(s)

答案就是 map.values()

很正常的“分类装箱”： “按签名丢进对应的桶里”。

思路二：26 维频次数组当“签名”（更偏底层一点）

因为题目说只包含小写字母 a-z，那每个字符串可以用一个长度为 26 的数组描述它：

count[0]：字母 'a' 出现次数
count[1]：字母 'b' 出现次数
……

比如 "eat"：

e → 第 4 位 +1
a → 第 0 位 +1
t → 第 19 位 +1

得到一个数组，转成元组 (…)，当 key。同一组异位词的频次数组肯定一模一样。

好处：

不用排序了，单个串复杂度 O(L)
总体复杂度：O(N * L)，比排序版略好一点

坏处：

比较丑，不如排序版直观
面试时看心情，两种都可以

✅ Python 代码：排序版（推荐，先写这个）

from typing import List
from collections import defaultdict

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        groups = defaultdict(list)  # key: 排序后的字符串, value: 同组的原字符串列表

        for s in strs:
            # 排序后作为“签名”
            key = ''.join(sorted(s))
            groups[key].append(s)
        
        # 返回所有分组即可
        return list(groups.values())

✅ Python 代码：计数版（进阶一点）

from typing import List
from collections import defaultdict

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        groups = defaultdict(list)

        for s in strs:
            count = [0] * 26
            for ch in s:
                count[ord(ch) - ord('a')] += 1
            
            # 数组不能做 key，用 tuple
            key = tuple(count)
            groups[key].append(s)
        
        return list(groups.values())

🧩 核心逻辑表

以“排序版”为例：

当前字符串 `s`	排序结果 `key`	放入哈希表中的分组
`"eat"`	`"aet"`	`groups["aet"] = ["eat"]`
`"tea"`	`"aet"`	`groups["aet"] = ["eat", "tea"]`
`"tan"`	`"ant"`	`groups["ant"] = ["tan"]`
`"nat"`	`"ant"`	`groups["ant"] = ["tan", "nat"]`
`"bat"`	`"abt"`	`groups["abt"] = ["bat"]`

最后把 groups 的所有 value 抽出来，就是答案。

⏳ 复杂度分析

排序版

设 N = strs.length，K = 字符串平均长度
时间复杂度：
- 每个字符串要排序：O(K log K)
- 总体：O(N * K log K)
空间复杂度：
- 存哈希表，几乎把所有字符串都装进去
- 额外存 key，整体是 O(N * K)

计数版

时间复杂度：
- 每个字符串只扫一遍：O(K)
- 总体：O(N * K)
空间复杂度：同样 O(N * K) 量级

🪄 小结口诀

异位词组要分家，
长相不同骨架同。

排序签名最好写，
计数签名更高效。

签名当键进字典，
一键打包成分组。

✅ 关键词记忆：哈希分组、排序作为签名、26 维频次数组、defaultdict(list)

这一题就是典型的“看到分组 + 异位词 → 条件反射想到哈希表”那一挂，你刚才问了半天哈希表底层，现在这题正好拿来实战巩固，挺顺。

补充：本题哈希表底层原理

行，你这么问，说明终于决定善待一下自己的大脑了，非常好 😏

我用几个小图给你“捋顺”哈希表到底长什么样。

1️⃣ 整体结构长啥样？

逻辑上你看到的是字典 / map：

key → value
"eat" → 0
"tea" → 1
"tan" → 2
...

底层其实是：

          哈希函数
 key  ─────────────▶  某个桶下标

                ┌─────────────────────────────┐
buckets[0]  →   │   空                        │
buckets[1]  →   │   ("abt") → ["bat"]         │
buckets[2]  →   │   空                        │
buckets[3]  →   │   ("ant") → ["tan","nat"]   │
buckets[4]  →   │   空                        │
buckets[5]  →   │   ("aet") → ["eat","tea"]   │
buckets[6]  →   │   空                        │
buckets[7]  →   │   空                        │
                └─────────────────────────────┘

这里你可以把它想象成：

底层是一个数组 buckets
每个 buckets[i] 是一个“桶”
每个桶里存若干 (key → value) 映射，可能是链表、数组之类

2️⃣ 具体走一遍插入过程

拿你刚做的“字母异位词分组”那题举个例子，我们用排序后的字符串做 key：

数据是：

1	["eat", "tea", "tan", "ate", "nat", "bat"]

我们构造哈希表：key = 排序后的字符串，value = 这一组单词列表

第一步：插 `"eat"`

原串："eat"
key：排序后 "aet"

交给哈希表：

1	h("aet") = 5 （假装哈希函数算出来是 5）

插进去后：

index:   0        1        2        3        4        5          6        7
        ┌───┬────────┬────────┬────────┬────────┬────────────┬────────┬────────┐
bkt[i]: │   │        │        │        │        │ ("aet")    │        │        │
        │   │        │        │        │        │  ["eat"]   │        │        │
        └───┴────────┴────────┴────────┴────────┴────────────┴────────┴────────┘

第二步：插 `"tea"`

原串："tea"
key："aet"

哈希表过程：

1	h("aet") = 5 （同一个 key，hash 值一样）

发现桶 5 已经有 key "aet"，那就在该 key 对应的列表后面 append：

index:   0        1        2        3        4        5                    6        7
        ┌───┬────────┬────────┬────────┬────────┬─────────────────────┬────────┬────────┐
bkt[i]: │   │        │        │        │        │ ("aet")             │        │        │
        │   │        │        │        │        │  ["eat","tea"]      │        │        │
        └───┴────────┴────────┴────────┴────────┴─────────────────────┴────────┴────────┘

第三步：插 `"tan"`

原串："tan"
key："ant"

1	h("ant") = 3

于是桶 3 新开一组：

index:   0        1        2        3                4        5                    6        7
        ┌───┬────────┬────────┬────────────────┬────────┬─────────────────────┬────────┬────────┐
bkt[i]: │   │        │        │ ("ant")        │        │ ("aet")             │        │        │
        │   │        │        │  ["tan"]       │        │  ["eat","tea"]      │        │        │
        └───┴────────┴────────┴────────────────┴────────┴─────────────────────┴────────┴────────┘

继续插 "nat" 时，key 也是 "ant"，就挂到同一组里。

插 "bat" 时，key 是 "abt"，哈希到另一个桶，比如 1：

index:   0        1                 2        3                     4        5                       6        7
        ┌───┬─────────────────┬────────┬────────────────────┬────────┬────────────────────────┬────────┬────────┐
bkt[i]: │   │ ("abt")         │        │ ("ant")            │        │ ("aet")                │        │        │
        │   │  ["bat"]        │        │  ["tan","nat"]     │        │  ["eat","tea","ate"]   │        │        │
        └───┴─────────────────┴────────┴────────────────────┴────────┴────────────────────────┴────────┴────────┘

这就是你最后 defaultdict(list).values() 时看到的三组结果。

3️⃣ 再抽象一下“一查一存”的流程

对你写题来说，最关键的不是底层怎么 malloc 的，而是这套套路：

插入（`mp[key].append(x)`）脑内流程：

1. 算哈希：h = hash(key)
2. 定位桶：idx = h % capacity
3. 在 buckets[idx] 里：
   - 如果 key 已存在：更新 / append
   - 否则：新建一条记录 (key → value)

查询（`key in mp` 或 `mp[key]`）脑内流程：

1. 算哈希：h = hash(key)
2. 定位桶：idx = h % capacity
3. 在 buckets[idx] 里找有没有这个 key
   - 有：取出它的 value
   - 没有：说明 key 不在表里

你可以把哈希表想成： “一群桶，外加一个算 key 应该住在哪个桶里的函数。”

4️⃣ 和你正在刷的题绑定一下

两数之和： mp[value] = index → 哈希表长得像：值 → 下标
字母异位词分组： mp[签名] = [同组字符串列表] → 哈希表长得像："aet" → ["eat","tea","ate"]

🔢 最长连续序列（Longest Consecutive Sequence）

做题次数	做题时间	做题结果
第一次	2025.12.02	记住了“哈希存全集，只从起点数”的套路，能默写 O(n) 解法

🧩 题目描述

给定一个未排序的整数数组 nums，找出其中数字连续的最长序列的长度。

序列里的数字必须是数值上连续，比如 1,2,3,4
不要求在原数组中下标连续
要求算法时间复杂度为 O(n)

📌 示例

示例 1

输入：

1	nums = [100, 4, 200, 1, 3, 2]

输出：

解释：最长连续序列是 [1, 2, 3, 4]，长度为 4。

示例 2

输入：

1	nums = [0,3,7,2,5,8,4,6,0,1]

输出：

解释：最长连续序列是 [0,1,2,3,4,5,6,7,8]，长度为 9。

示例 3

输入：

1	nums = [1,0,1,2]

输出：

解释：最长连续序列是 [0,1,2]，长度为 3（注意有重复元素，但不影响结果）。

🧠 解题思路：哈希表 + “只从起点开始数”

要求 **O(n)**，直接把排序解法干掉：

排序再一趟扫描是 O(n log n)，不符合要求，只能当热身。

真正的做法是：

把所有数丢进哈希集合里，然后只在“连续段的起点”往右数。

具体步骤：

把所有元素放进集合
1
s = set(nums)
这样我们可以 O(1) 判断某个数是否存在。
遍历集合中的每个数 x，判断它是不是“连续段的起点”：
- 如果 x - 1 不在集合里，说明：
  - x 前面没有 x-1
  - 那 x 就是一个连续序列的起点
- 如果 x - 1 在集合里，说明从 x 开始数会“从中间切入”，这种就直接跳过。
从起点开始一路往右数：
- 对每个起点 x：
  - 设 current = x
  - 一直判断 current + 1 是否在集合里
  - 在的话就 current += 1，长度 length += 1
- 把这段连续区间的长度和全局 longest 比较，更新最大值。
处理边界：
- 如果 nums 为空，直接返回 0。

核心心法一句话：

“哈希存全集，只从起点数一遍，每个数最多被数一次。”

这样整个过程是 O(n)。

✅ Python 代码（类方法版）

class Solution:
    def longestConsecutive(self, nums: list[int]) -> int:
        if not nums:
            return 0

        num_set = set(nums)   # 哈希表：存全集
        longest = 0

        for x in num_set:
            # 只有当 x-1 不在集合中时，x 才可能是一个连续序列的起点
            if x - 1 not in num_set:
                current = x
                length = 1

                # 一路往右数：x, x+1, x+2, ...
                while current + 1 in num_set:
                    current += 1
                    length += 1

                longest = max(longest, length)

        return longest

🪄 核心逻辑状态表

以示例 nums = [100, 4, 200, 1, 3, 2] 为例：

哈希集合：{1, 2, 3, 4, 100, 200}

当前数 x	x-1 在集合中？	是不是起点？	从 x 开始数到的序列	序列长度
1	0 不在	✅ 起点	1,2,3,4	4
2	1 在	❌ 不是	跳过	-
3	2 在	❌ 不是	跳过	-
4	3 在	❌ 不是	跳过	-
100	99 不在	✅ 起点	100	1
200	199 不在	✅ 起点	200	1

全局最长长度 longest = 4。

注意到：

每个数只会被当作“起点”检查一次
每个数也只会在某个连续序列中被“往右数”到一次整体访问次数是线性的。

⏳ 复杂度分析

时间复杂度：
- 建集合：O(n)
- 遍历集合 + 往右数：每个数最多被访问两次级别，整体 O(n)
- 总计：O(n)
空间复杂度：
- 需要一个哈希集合存所有元素
- O(n)

🧾 小结口诀

哈希存全集，
只从起点起。
一路向右数，
最长即所求。

✅ 关键词记忆：哈希集合、只从起点数、O(n)、去重不影响结果

双指针

🚚 移动零（Move Zeroes）

做题次数	做题时间	做题结果
第一次	2025.12.04	记住快慢指针“挤前面、丢后面”，会写原地 O(1) 解法

🧩 题目描述

给定一个数组 nums，将所有的 0 移动到数组末尾，同时保持非零元素的相对顺序不变。

要求：原地修改数组，不允许额外开一个同等大小的数组拷贝。

📌 示例

示例 1

输入：

1	nums = [0, 1, 0, 3, 12]

输出（原地修改后）：

1	[1, 3, 12, 0, 0]

示例 2

输入：

1	nums = [0]

输出：

[0]

🧠 解题思路：快慢指针，把非零“挤”到前面

核心模型：快慢指针（双指针），一趟扫描原地完成。

思路拆开讲：

维护两个指针：
- fast：从左到右扫描整个数组。
- slow：指向“下一个应该放非零数的位置”。
遍历数组：
- 每当 nums[fast] != 0：
  - 把 nums[fast] 挪到 nums[slow] 的位置（用交换实现）
  - slow += 1
- 当前元素是 0：fast 继续往右走，不理它。
为啥能保持相对顺序？
- 非零元素是按原出现顺序，被依次丢到 0,1,2,... 这些前面的位置里。
- 只是在遇到 0 时不动 slow，相当于前面“留坑”，等后面的非零来填。
为啥能把 0 移到末尾？
- 所有非零都被稳定挤到前面 [0..slow-1]
- 后面的尾部自然就只剩下被换过去的 0。
进阶：减少操作次数
- 当 slow == fast 时，其实不需要交换，因为元素本来就在该在的位置上。
- 所以可以加条件：只有 slow != fast 才交换，减少无意义写入。

✅ Python 代码（类方法版，原地修改）

from typing import List

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        slow = 0  # 下一个非零要放的位置

        for fast in range(len(nums)):
            if nums[fast] != 0:
                # 只有 slow 和 fast 不同时才交换，减少不必要写操作
                if slow != fast:
                    nums[slow], nums[fast] = nums[fast], nums[slow]
                slow += 1

🧪 指针移动过程示意（示例 1）

以 nums = [0, 1, 0, 3, 12] 为例：

步骤	fast	slow	当前 nums	操作说明
初始	-	0	[0, 1, 0, 3, 12]	开始遍历
1	0	0	[0, 1, 0, 3, 12]	nums[0]=0，跳过
2	1	0	[1, 0, 0, 3, 12]	非零，交换 nums[0], nums[1]
		1	[1, 0, 0, 3, 12]	slow → 1
3	2	1	[1, 0, 0, 3, 12]	nums[2]=0，跳过
4	3	1	[1, 3, 0, 0, 12]	非零，交换 nums[1], nums[3]
		2	[1, 3, 0, 0, 12]	slow → 2
5	4	2	[1, 3, 12, 0, 0]	非零，交换 nums[2], nums[4]
		3	[1, 3, 12, 0, 0]	结束

最终得到 [1, 3, 12, 0, 0]。

⏳ 复杂度分析

时间复杂度：O(n)
单次线性扫描，每个元素最多参与一次交换。
空间复杂度：O(1)
只用了常数级的若干指针变量，原地修改数组。

🪄 小结口诀

快指针全遍历，
慢指针挤前排。
非零就换上，
零被丢后排。

✅ 关键词记忆：原地操作、快慢指针、稳定顺序、只挤非零

🪣 盛最多水的容器（Container With Most Water）

做题次数	做题时间	做题结果
第一次	2025.12.04	记住双指针“从两边夹，永远挪短板”，能默写 O(n) 解法

🧩 题目描述

给定一个长度为 n 的整数数组 height，其中有 n 条竖线：

第 i 条线的两个端点是 (i, 0) 和 (i, height[i])
任意选择两条线和 x 轴，可以形成一个“装水的容器”

目标：找出一对线，使得形成的容器可以装的水最多，并返回这个最大水量。

注意：

不能倾斜容器
容量由宽度 × 较短的那条线高度决定

📌 示例

示例 1

输入：

1	height = [1,8,6,2,5,4,8,3,7]

输出：

解释：

选择下标 1 和 8：
- 高度分别为 8 和 7
- 宽度为 8 - 1 = 7
- 水量为 min(8, 7) * 7 = 7 * 7 = 49
这是所有选择中最大的水量。

示例 2

输入：

1	height = [1,1]

输出：

解释：只能选两条线，高度都是 1，宽度 1，结果为 1 * 1 = 1。

🧠 解题思路：双指针 + 挪短板

暴力做法是：枚举所有两条线，计算面积，时间复杂度 O(n^2)，会超时，不要写在面试里。

想要 O(n)，套路是：

从两端开始，用双指针夹逼，每次移动“较短的那一边”。

具体做法：

定义两个指针：
- left = 0 指向最左边
- right = n - 1 指向最右边
当前容器的面积：
- 宽度 width = right - left
- 高度是两条线中较小的那个：h = min(height[left], height[right])
- 当前面积 area = h * width
如何移动指针？关键决策点：
- 总体目标：让短板尽量变高，因为高度由短板决定。
- 如果：
  - height[left] < height[right]
    说明左边是短板，再往右缩小宽度的同时，只可能通过右移 left来争取更高的短板。
  - height[left] > height[right]
    说明右边是短板，要想变高就左移 right。
  - 相等时，随便移动一边都可以，一般移任意一边。
核心直觉：

当前面积由短板决定，如果我移动长板，只会让宽度变小，而高度上限仍然被短板卡住，面积只会更小，不可能更大。
所以每一步只移动短板，才有“潜在变大”的机会。
遍历过程：
- 每一步更新一次最大面积 max_area
- 然后移动短板指针
- 直到 left >= right，所有可能的“有效组合”都被考虑到。

✅ Python 代码（类方法版）

from typing import List

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left, right = 0, len(height) - 1
        max_area = 0

        while left < right:
            h = min(height[left], height[right])
            width = right - left
            area = h * width
            if area > max_area:
                max_area = area

            # 移动短板那一边
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1

        return max_area

🧪 指针移动过程示意（示例 1）

1	height = [1,8,6,2,5,4,8,3,7]

步骤	left	right	height[left]	height[right]	宽度	当前面积	谁更短	移动谁
1	0	8	1	7	8	`1 * 8 = 8`	左	left++
2	1	8	8	7	7	`7 * 7 = 49`	右	right–
3	1	7	8	3	6	`3 * 6 = 18`	右	right–
4	1	6	8	8	5	`8 * 5 = 40`	任意	right–
5	1	5	8	4	4	`4 * 4 = 16`	右	right–
6	1	4	8	5	3	`5 * 3 = 15`	右	right–
7	1	3	8	2	2	`2 * 2 = 4`	右	right–
8	1	2	8	6	1	`6 * 1 = 6`	右	right–

最终最大面积为 49。

⏳ 复杂度分析

时间复杂度：
整个过程每次只移动一个指针，left 从左到右，right 从右到左，最多各走一遍，整体 O(n)。
空间复杂度：
使用了常数级变量，O(1)。

🪄 小结口诀

两端起指针，
面积看短板。
短板向内缩，
一路保最大。

✅ 关键词记忆：双指针、挪短板、宽度 × 短板高度、O(n)

🔺 三数之和（3Sum）

做题次数	做题时间	做题结果
第一次	2025.12.08	掌握“排序 + 固定一位 + 双指针 + 跳重”，能写出去重版 O(n²)

🧩 题目描述

给定一个整数数组 nums，判断其中是否存在三元组 [nums[i], nums[j], nums[k]] 满足：

i != j、i != k、j != k
nums[i] + nums[j] + nums[k] == 0

要求返回所有和为 0 且不重复的三元组。

注意：

三元组内部的数顺序无所谓
结果列表中不能出现重复三元组

📌 示例

示例 1

1	nums = [-1, 0, 1, 2, -1, -4]

输出：

1	[[-1, -1, 2], [-1, 0, 1]]

解释：所有和为 0 的不同三元组有：

[-1, -1, 2]
[-1, 0, 1]

示例 2

1	nums = [0, 1, 1]

输出：

[]

解释：不存在三数之和为 0 的三元组。

示例 3

1	nums = [0, 0, 0]

输出：

1	[[0, 0, 0]]

解释：唯一合法三元组是 [0, 0, 0]。

🧠 解题思路：排序 + 固定一数 + 双指针扫两数

核心套路：

先排序，再固定一个数，把问题变成“有序数组中的两数之和”问题，用双指针解决，同时注意去重。

具体步骤：

数组排序
1
nums.sort()
这样相同元素会挨在一起，方便跳过重复，避免重复三元组。
枚举第一个数 nums[i]
- 下标 i 从 0 到 n-3
- 为了避免重复的三元组：
  - 当 i > 0 且 nums[i] == nums[i - 1] 时，直接 continue
    因为这个值作为起点已经处理过了。
在剩下区间内做“两数之和”

对固定的 i，我们在右侧区间 [i+1, n-1] 内找两个数，使得：
1
2
nums[i] + nums[left] + nums[right] == 0
⇔ nums[left] + nums[right] == -nums[i]
用两个指针：
- left = i + 1
- right = n - 1
然后在区间内夹逼：
- 如果和小于 0：需要变大 → left += 1
- 如果和大于 0：需要变小 → right -= 1
- 如果和等于 0：
  - 记录当前三元组
  - 然后要跳过重复的 left / right 值，避免重复三元组
  - 再同时移动 left += 1，right -= 1，继续找下一组
去重关键点
- 外层 for i：如果 nums[i] == nums[i-1]，跳过
- 内层双指针：
  - 当找到一组合法解 (nums[i], nums[left], nums[right]) 后：
    - left 往右跳过所有与当前 nums[left] 相同的数
    - right 往左跳过所有与当前 nums[right] 相同的数
这样可以保证输出结果中，每种数值组合只出现一次。
长度小于 3 可以直接返回空

✅ Python 代码（类方法版）

from typing import List

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        n = len(nums)
        res: List[List[int]] = []

        for i in range(n):
            # 第一个数去重：相同起点会产生重复三元组
            if i > 0 and nums[i] == nums[i - 1]:
                continue

            # 剪枝：如果当前 nums[i] > 0，后面都 ≥ 它，不可能和为 0
            if nums[i] > 0:
                break

            left, right = i + 1, n - 1
            target = -nums[i]

            while left < right:
                s = nums[left] + nums[right]
                if s == target:
                    res.append([nums[i], nums[left], nums[right]])

                    # 左指针去重
                    left_val = nums[left]
                    while left < right and nums[left] == left_val:
                        left += 1

                    # 右指针去重
                    right_val = nums[right]
                    while left < right and nums[right] == right_val:
                        right -= 1

                elif s < target:
                    left += 1
                else:
                    right -= 1

        return res

🧮 核心逻辑小表（以示例一为例）

1 2	nums = [-1,0,1,2,-1,-4]` 排序后：`[-4, -1, -1, 0, 1, 2]

i	nums[i]	left/right 初始	可能找到的三元组	说明
0	-4	L=1, R=5	无	-4 过小，组合都 < 0
1	-1	L=2, R=5	[-1, -1, 2]	-1 + -1 + 2 = 0
		L=3, R=4	[-1, 0, 1]	-1 + 0 + 1 = 0
2	-1	跳过	-	与 nums[1] 相同，避免重复起点
3	0	L=4, R=5	无	0 + 1 + 2 > 0，右移，结束
4	1	后面不够两个数	结束

最终结果：[[-1, -1, 2], [-1, 0, 1]]

⏳ 复杂度分析

时间复杂度：
- 排序 O(n log n)
- 外层固定 i，内层双指针整体是 O(n²)
- 总体：**O(n²)**（主导项）
空间复杂度：
- 排序为原地排序（视实现可认为额外空间 O(1)）
- 只使用了常数级辅助变量
- 不考虑返回结果，本身额外空间：**O(1)**

🪄 小结口诀

先排好顺序，
一位定起点。
两指左右逼，
小加左，大减右。
相等收答案，
左右跳重值。

✅ 关键词记忆：排序、固定一数、双指针、去重、O(n²)

🌧 42. 接雨水（Trapping Rain Water）

做题次数	做题时间	做题结果
第一次	2025.12.08	记住“横向看水位：两边取小，减掉自己”+ 双指针 O(1) 模板

🧩 题目描述

给定 n 个非负整数，表示宽度为 1 的柱子的高度图 height，计算下雨之后，这些柱子之间能接多少雨水。

每根柱子视为一个宽度为 1 的竖条，相邻竖条之间可能形成“坑”，水会积在这些坑里。

📌 示例

示例 1

1	height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出：

解释：如图，这些柱子之间总共能接 6 单位的水。

示例 2

1	height = [4,2,0,3,2,5]

输出：

🧠 解题思路：水位取决于左右最高柱

直觉模型：每一格能存多少水，取决于它左边最高柱和右边最高柱中的较小值，与自己高度的差值。

对任意位置 i：

left_max[i]：位置 i 左边（含自己）的最高高度
right_max[i]：位置 i 右边（含自己）的最高高度
那么位置 i 上方的水位是：

$$
water_level[i] = \min(left_max[i],\ right_max[i])
$$

真正的存水量：

$$
water[i] = \max\big(0,\ \min(left_max[i], right_max[i]) - height[i]\big)
$$

整题就是把所有 water[i] 加起来。

解法一：前后缀数组（好理解版，O(n) 空间）

预处理数组：
- 从左到右：算 left_max[i]
- 从右到左：算 right_max[i]
再遍历一遍数组：
- 对每个 i，按上面公式算 water[i]，累加。

这个很好理解，但要用 O(n) 的空间。

解法二：双指针 + 动态维护左右最大（O(1) 空间重点）

更优雅的版本，用双指针 + 两个变量代替整两个数组。

思路：

两个指针：
- left = 0
- right = n - 1
两个变量记录当前扫描到的左侧最高和右侧最高：
- left_max = 0
- right_max = 0
核心结论：

当 height[left] < height[right] 时：

此时左边这一侧的最大水位由 left_max 和 height[right] 中的较小值决定，
但因为 height[left] < height[right]，对 left 来说，右侧至少有个 height[right] 这么高的墙，
所以短板一定在左边，水位取决于 left_max。

于是：
- 如果 height[left] >= left_max：
  - 更新 left_max = height[left]
- 否则：
  - ans += left_max - height[left]（这一格能存的水量）
- 然后 left += 1
反之，当 height[left] >= height[right] 时，同理处理右侧：
- 如果 height[right] >= right_max：
  - 更新 right_max = height[right]
- 否则：
  - ans += right_max - height[right]
- 然后 right -= 1
终止条件：left >= right

一句话心法：

谁矮，谁那一侧的水位就能确定，就处理谁。

✅ Python 代码（双指针 O(1) 空间）

from typing import List

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        if n <= 2:
            return 0  # 至少要三根柱子才能形成“坑”

        left, right = 0, n - 1
        left_max, right_max = 0, 0
        ans = 0

        while left < right:
            if height[left] < height[right]:
                # 左侧更矮，左边的水位可以由 left_max 决定
                if height[left] >= left_max:
                    left_max = height[left]
                else:
                    ans += left_max - height[left]
                left += 1
            else:
                # 右侧更矮，右边的水位可以由 right_max 决定
                if height[right] >= right_max:
                    right_max = height[right]
                else:
                    ans += right_max - height[right]
                right -= 1

        return ans

🪜 核心状态小表（示例一简化示意）

1	height = [0,1,0,2,1,0,1,3,2,1,2,1]

只看指针与水量变化的逻辑（略去全部细节）：

步骤	left	right	left_max	right_max	当前处理哪边	新增水量
初始	0	11	0	0	-	0
1	0	11	0	1	右	0
2	0	10	0	2	右	0
3	0	9	0	2	右	`2 - 1 = 1`
4	0	8	0	2	右	`2 - 2 = 0`
5	0	7	0	3	右	`3 - 3 = 0`
6	0	7	0	3	左	`0 - 0 = 0`
7	1	7	1	3	左	`1 - 1 = 0`
8	2	7	1	3	左	`1 - 0 = 1`
9	3	7	2	3	左	`2 - 2 = 0`
…	…	…	…	…	…	…

最终累加得到总水量 6。

⏳ 复杂度分析

时间复杂度：
整个数组只被双指针从两头扫一遍
→ O(n)
空间复杂度：
只用了常数级变量 left, right, left_max, right_max, ans
→ O(1)

🪄 小结口诀

单柱存水量，
左右高取小。
水高减自身，
遍历全加和。

谁矮算谁边，
水位被锁定。
双指针夹逼，
O(1) 空间行。

✅ 关键词记忆：每格水 = min(左最大, 右最大) - 自身、双指针、谁矮动谁、O(n) + O(1)

好，你要的是「双指针总复盘讲义版」对吧，那我给你整一份可以反复回看的笔记。以后面试前翻一眼，心里有数。

🧷 双指针套路总总结笔记

1. 四道题的共同特征（为什么它们都适合双指针）

这四题有几个非常明显的共性，可以当“识别信号”：

① 输入结构：一维线性序列

全都是：数组 + 下标 i
没有乱七八糟图/树/矩阵，本质是一条线上的问题

双指针经典适用场景：数组 / 字符串这种一维线性结构

② 需求和“元素间关系”有关

Move Zeroes：保持非零元素相对顺序，把 0 推到后面
Container：任意选两根柱子，比较哪一对面积最大
3Sum：选三数，转化为“固定一位 + 两数之和”
接雨水：每一格的水量由左右边界高度决定

本质都是：

“在一条线上，不同位置之间的关系决定答案。”

③ 暴力一写就爆炸

如果你不加思考，最自然写法：

Move Zeroes：每遇到 0 就整体挪一段 → 可能 O(n^2)
Container：枚举所有 (i, j) → O(n^2)
3Sum：三重循环 i, j, k → O(n^3)
接雨水：对每个 i，向左向右扫最大值 → O(n^2)

题目数据范围都不小，暴力一脸“超时预定”的样子，明显在暗示你优化。

④ 存在“单调推进、不回头”的机会

双指针的灵魂是：

指针移动的过程中，有某个量是单调变化的，
所以不需要回头，也不会漏掉正确答案。

在这四题里分别是：

Move Zeroes：fast 从左到右一次遍历；slow 只前进不后退
Container：left 从 0 到右移，right 从 n-1 左移，区间只会缩小
3Sum：
- 外层 i 从左到右
- 内层 two-sum：left++ / right--，只往里走
接雨水：left、right 一路往中间靠拢，同时维护 left_max/right_max

⑤ 目标复杂度：O(n) 或 O(n²) + O(1) 空间

Move Zeroes：O(n)，原地修改
Container：O(n)，双指针扫一遍
3Sum：排序 O(n log n) + 枚举 i + 双指针 O(n²)
接雨水：O(n)，双指针 + O(1) 状态

遇到类似约束时，可以优先怀疑有双指针 / 滑动窗口之类的线性扫描优化。

2. 如何识别一道题“可能用双指针”

给你一个小 checklist，刷题时可以在脑子里快速过一遍：

是不是一维结构？
- 数组 / 字符串 / 有序表
- 是的话，双指针/滑动窗口优先级升高
需求是不是和区间 / 两个端点 / 两数或者三数关系有关？
- 找两数/三数；
- 找满足条件的最长/最短子数组；
- 调整元素位置但保持顺序；
- 按左右边界定义某种“值”。
暴力是不是很自然但复杂度太高？
- 你一上来就想写两重或三重循环
- 那很有可能有“用双指针把内层单调化”的版
能不能通过排序或前后缀，让一些判断变成“单调的”？
- 3Sum：排序后，two-sum 调整和的大小能用 left++ / right--
- 容器：宽度在缩小，高度由短板控制，移动长板永远不优
- 接雨水：height[left] < height[right] 时，左边水位只受 left_max 限制
能不能这样刻画：

“假设我枚举第一层 i，
第二层 j 不需要每次从头来，只需要接着往后/往前走？”

如果你能给出一种不回头的 j 的移动方式，那就是典型双指针场景。

3. 双指针的题目类型：三大类

① 同向双指针 / 快慢指针（压缩、过滤型）

代表：Move Zeroes

指针方向一致：fast、slow 都向右走
职责分工：
- fast：完整扫描，用来“发现”元素
- slow：指向“下一个有效元素应该放的位置”

典型伪代码：

slow = 0
for fast in range(n):
    if 是我们想保留的元素:
        nums[slow] = nums[fast]  # 或交换
        slow += 1
# slow 之后的区域随意处理（填0、截断等）

应用：

移除元素、移除重复、稳定保序地压缩数组
滑动窗口的一种特殊形式
链表中快慢指针找中点、判环

② 对向双指针（从两端夹）

代表：

盛最多水的容器
接雨水（虽然更复杂一点）
3Sum 内层 two-sum

基本模式：

left, right = 0, n - 1
while left < right:
    # 根据当前状态做一些计算
    if 某种条件:
        left += 1
    else:
        right -= 1

用法：

在有序数组里做两数之和（two-sum）
在“一维上两端是边界”的物理模型中（盛水、雨水等）
在“区间收缩”的问题中，用条件决定缩哪边

③ 外层枚举 + 内层双指针（K-Sum 原型）

代表：3Sum

套路非常标准：

排序 nums.sort()
for i 枚举第一个数（适当剪枝 + 去重）
在 [i+1, n-1] 上，用双指针做 two-sum

结构：

for i in range(n):
    # 去重 / 剪枝
    left, right = i+1, n-1
    while left < right:
        s = nums[i] + nums[left] + nums[right]
        # 然后根据 s 与 0 的关系决定 left++ / right--

这是很多题的母版，比如：

3Sum
4Sum（再套一层）
找三元组最接近 target 等

4. 双指针的核心思路：两大心法

① 同向双指针心法：“快指针探路，慢指针落位”

把数组想象成一条传送带：

快指针：扫描整个数组，负责“发现好东西”
慢指针：维护前半段是“已经排好/压缩好”的区域

核心动作：

每当 fast 遇到一个需要保留的元素，
就丢到 slow 的位置，slow++。

Move Zeroes 就是：

遇到非 0 的数，往前挤
slow 之前都是非 0，顺序不变
slow 之后自然全是 0（被换到后面去了）

② 对向双指针心法：“谁矮 / 谁小 / 谁劣，就动谁”

具体表现在：

two-sum / 3Sum 内层：
- 排序后：
  - 当前 sum < target：想变大 → left++
  - 当前 sum > target：想变小 → right--
- 因为：
  - 右边再往右？不存在
  - 左边再往左？也没救
  - 只有靠近中间，才可能调节和
盛最多水的容器：
- 面积 = 宽度 × 短板高度
- 要面积变大，只能指望短板变高
- 移动长板只会减宽度、短板不变 → 永不优
- 所以：每次只移动短板那一侧
接雨水：
- 若 height[left] < height[right]：
  - 短板在左侧
  - 左边这一格的水位由 left_max 决定
  - 右边再怎么高也不会影响这格
  - 所以可以安全结算 left 的水量，left++

统一成一句话：

每次都用“比较结果”排除一整片不可能贡献更优解的状态，
然后只动一边指针，让某个量单调变化（和 / 宽度 / 水位 / 区间）。

5. 双指针题的难点 & 突破点

难点 1：你凭什么敢动它？

核心问题：

“我每次移动指针，都在放弃一堆可能的 (i, j)，
凭什么说，这些被放弃的组合里一定不会有更优解？”

突破点：
每道双指针题都要给自己一个 “数学借口”，比如：

容器：移动长板 → 宽度减小，短板不变 → 面积不可能变大
two-sum：当前 sum < target 时再减右边只会更小，没意义
接雨水：左矮右高时，这格的短板一定在左边，水位只跟 left_max 有关

你做到的标准是：

不再只是“记住要移动哪边”，而是能解释：
“我这样移动，砍掉的那一块一定是垃圾解。”

难点 2：看不出可以用双指针

突破点：用“暴力 → 降维”思路

先承认：暴力要怎么写？
- 两重循环 / 三重循环
问自己：

“能不能把第二层循环变成一个单调移动的指针，
让它不回头，把所有情况都扫完？”

能做到这点的关键往往是：

排序 → 引入单调性
或者找到某种“性质”使得：
- left++ 只会让和变大
- right-- 只会让和变小
- 宽度只会变小
- 某个 max/min 只会单调更新

难点 3：边界、去重、越界

典型坑点：

while left < right vs <=
i 要不要从 0 到 n-3？
3Sum 里：
- i 的去重
- 找到解后 left 的去重
- right 的去重
  少一个都乱套
滑动窗口题：左/右指针何时移动、窗口大小怎么算，+1 / 不 +1 总有人写翻车

突破点：

写完一定要配一个小样本 + 状态表，手动跑一遍。

比如：

3Sum 用 [-1, 0, 1, 2, -1, -4] 跑
雨水用 [3, 0, 2, 0, 4] 跑
盛水用 [1,8,6,2,5,4,8,3,7] 跑前几步

难点 4：各种形式看起来碎

突破点：把它们归类成“模式”而不是一道道记：

Move Zeroes：
→ 同向快慢指针，压缩数组型
Container / two-sum / 3Sum 内层：
→ 对向双指针，根据比较结果决定移动哪边
接雨水：
→ 对向双指针 + 左右状态（left_max/right_max）

以后遇到新题，你要想的是：

“它更像 Move Zeroes 这种，还是像 two-sum，还是像接雨水这种带状态的对向指针？”

6. 最后给自己留一张脑内小抄

可以记成四句话：

1. 识别：
   一维结构 + 区间/配对/三数关系 + 要求 O(n)/O(n²)，优先想双指针。

2. 模式：
   同向（快慢/窗口）、
   对向（两端夹）、
   外层枚举 + 内层对向。

3. 正确性：
   每次移动指针前，问自己：
   “我砍掉的这部分状态，为什么一定不可能更优？”

4. 细节：
   写完用一个小例子 + 简单表格，把指针动几步，
   看有没有漏解、重复、越界。

这份笔记你随便存哪，本质上你已经有了一个：

“双指针通用心智模型”，
而不只是“会几道题”。

后面再遇到类似题型，你只需要对照这几类模式，往里一套，然后改局部细节就行。
剩下的就是多写几题把手感练熟，脑子和手同时在线，就挺无敌的了。

滑动窗口

🔐 无重复字符的最长子串（Longest Substring Without Repeating Characters）

做题次数	做题时间	做题结果
第一次	2025.12.09	掌握滑动窗口模板：用哈希表记录字符最新位置，动态收缩左边界

🧩 题目描述

给定一个字符串 s，请你找出其中不含有重复字符的最长子串的长度。

子串：要求是连续的一段字符
不能有重复字符
只需要返回长度，不用返回具体子串

📌 示例

示例 1

1
2
3

输入: s = "abcabcbb"
输出: 3
解释: 无重复字符的最长子串是 "abc"（"bca"、"cab" 也可以），长度为 3

示例 2

1
2
3

输入: s = "bbbbb"
输出: 1
解释: 无重复字符的最长子串是 "b"

示例 3

输入: s = "pwwkew"
输出: 3
解释: 无重复字符的最长子串是 "wke"，长度为 3
注意 "pwke" 是子序列，不是子串

约束

0 <= s.length <= 5 * 10^4
s 由英文字母、数字、符号和空格组成

🧠 解题思路：滑动窗口 + 字符最近出现位置

目标：找一个最长区间 [left, right]，区间内所有字符不重复。

用两个指针维护一个「滑动窗口」：

right 每次往右扩张，尝试把新字符加入窗口
若新字符在当前窗口中已经出现过，就移动 left 把旧位置「踢出窗口」

用一个哈希表 last_index 记录每个字符最近一次出现的位置：

初始化：
- left = 0 窗口左边界
- res = 0 记录答案
- last_index = {} 记录字符最近出现的下标
枚举 right：
- 设当前字符为 c = s[right]
- 如果 c 曾出现，并且它的上次出现位置在当前窗口内：
  - 把 left 移动到 last_index[c] + 1
  - 注意：left = max(left, last_index[c] + 1)，避免把左边界往回拉
- 更新 last_index[c] = right
- 更新当前窗口长度：res = max(res, right - left + 1)

👉 核心思想一句话：
右指针一直走，左指针只往右收缩，哈希表记录“重复字符”的上次位置，确保窗口内始终无重复。

✅ Python 代码（类方法版）

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        # last_index[c] 记录字符 c 最近一次出现的下标
        last_index = {}
        left = 0
        res = 0

        for right, ch in enumerate(s):
            # 如果 ch 在窗口内出现过，则收缩左边界
            if ch in last_index and last_index[ch] >= left:
                # 确保 left 只往右走
                left = last_index[ch] + 1

            # 更新当前字符最近出现位置
            last_index[ch] = right

            # 以当前 right 为右端的无重复子串长度
            res = max(res, right - left + 1)

        return res

🪄 核心逻辑表

情况	操作
新字符没出现过	直接扩大窗口，更新长度
字符出现过，但在窗口左侧外	视为没影响，窗口不收缩，只更新最近位置
字符出现过，且在窗口内	将 `left` 移到上次出现位置的右一位 `last_index[ch] + 1`
每一步更新答案	`res = max(res, right - left + 1)`

⏳ 复杂度分析

时间复杂度：O(N)
每个字符最多被左右指针访问各一次。
空间复杂度：O(min(N, Σ))
其中 Σ 为字符集大小，通过哈希表存储字符最近位置。

🧷 小结口诀

右指针扫全场，
左指针负责挡。
哈希记下旧坐标，
一旦重复左边涨。

✅ 关键词记忆：滑动窗口、哈希表、字符最近出现位置、left = max(left, last_index[ch] + 1)

🔡 找到字符串中所有字母异位词（Find All Anagrams in a String）

做题次数	做题时间	做题结果
第一次	2025.12.09	掌握固定长度滑动窗口 + 26 长度频次数组判断异位词

🧩 题目描述

给定两个字符串 s 和 p，找到 s 中所有 p 的字母异位词子串，返回这些子串的起始索引。

不考虑返回顺序
异位词：由相同字符和相同个数组成，但顺序可以不同

条件：

1 <= s.length, p.length <= 3 * 10^4
s 和 p 仅包含小写字母

📌 示例

示例 1

输入: s = "cbaebabacd", p = "abc"
输出: [0, 6]

解释:
索引 0 的子串 "cba" 是 "abc" 的异位词
索引 6 的子串 "bac" 也是 "abc" 的异位词

示例 2

输入: s = "abab", p = "ab"
输出: [0, 1, 2]

解释:
索引 0: "ab"  是异位词
索引 1: "ba"  是异位词
索引 2: "ab"  是异位词

🧠 解题思路：固定长度滑动窗口 + 频次数组

目标：在 s 里找出所有长度为 len(p) 的子串，使其刚好是 p 的一个异位词。

因为只包含小写字母，最舒服的做法就是用长度为 26 的数组统计频次：

cnt_p[26]：p 中每个字符出现次数
cnt_s[26]：当前窗口中每个字符出现次数

核心步骤

若 len(s) < len(p)，直接返回 []，根本塞不下一个异位词窗口。
设 m = len(p)：
- 先统计 p 的频次 cnt_p
- 统计 s[0..m-1] 的频次 cnt_s，这是第一个窗口
如果此时 cnt_s == cnt_p，说明从 0 开始就是一个异位词，记录 0。
从 right = m 开始往右滑动窗口：
- 窗口右边进来一个新字符 s[right]，频次 +1
- 窗口左边丢掉一个旧字符 s[left]，其中 left = right - m，频次 -1
- 滑完后当前窗口为 [left+1, right]（长度始终为 m）
- 如果 cnt_s == cnt_p，则 left+1 是一个异位词起点

因为每次只改两格数组，比较两个 26 长度数组的成本也是常数，总体是线性的。

👉 一句话：固定窗口长度 = len(p)，滑动时维护频次数组，数组相等的位置就是异位词起点。

✅ Python 代码（类方法版）

from typing import List

class Solution:
    def findAnagrams(self, s: str, p: str) -> List[int]:
        n, m = len(s), len(p)
        if n < m:
            return []

        res: List[int] = []
        cnt_p = [0] * 26
        cnt_s = [0] * 26

        # 统计 p 的频次 & s 的第一个窗口频次
        for i in range(m):
            cnt_p[ord(p[i]) - ord('a')] += 1
            cnt_s[ord(s[i]) - ord('a')] += 1

        # 检查初始窗口 [0, m-1]
        if cnt_s == cnt_p:
            res.append(0)

        # 滑动窗口
        for right in range(m, n):
            # 右边进一个字符
            idx_in = ord(s[right]) - ord('a')
            cnt_s[idx_in] += 1

            # 左边出一个字符
            left = right - m
            idx_out = ord(s[left]) - ord('a')
            cnt_s[idx_out] -= 1

            # 当前窗口 [left+1, right]
            if cnt_s == cnt_p:
                res.append(left + 1)

        return res

🪄 核心逻辑表

操作阶段	窗口范围	频次处理	判断条件
初始化窗口	`[0, m-1]`	统计 `p` 与 `s[0..m-1]` 的频次	`cnt_s == cnt_p`？
每次右移一步	`[left+1, right]`	新字符进窗口 +1，旧字符出窗口 -1	`cnt_s == cnt_p`？
满足异位词条件时	固定长度 `m` 的子串	当前窗口内频次与 `p` 的频次完全一致	记录起始下标

⏳ 复杂度分析

时间复杂度：O(|s| + |p|)
每个字符只进出窗口一次，比较两个长度 26 数组是常数。
空间复杂度：O(1)
只用到固定大小的 2 个频次数组。

🧷 小结口诀

长度固定窗滑跑，
进一出一频次调。
二十六格一对照，
相同下标全记好。

✅ 关键词记忆：固定长度滑动窗口、频次数组(26)、进一个出一个、cnt_s == cnt_p

➕ 560. 和为 K 的子数组（Subarray Sum Equals K）

做题次数	做题时间	做题结果
第一次	2025.12.11	掌握「前缀和 + 哈希表统计频次」，理解为什么不能用滑动窗口

🧩 题目描述

给你一个整数数组 nums 和一个整数 k，请你统计并返回和为 k 的子数组个数。

子数组：数组中元素的连续非空序列
元素可以为负数，所以不能用简单滑动窗口做「单调扩张」

📌 示例

示例 1

输入：nums = [1, 1, 1], k = 2
输出：2
解释：
子数组 [1,1]（前两个）
子数组 [1,1]（后两个）

示例 2

输入：nums = [1, 2, 3], k = 3
输出：2
解释：
子数组 [1,2]
子数组 [3]

约束

1 <= nums.length <= 2 * 10^4
-1000 <= nums[i] <= 1000
-10^7 <= k <= 10^7

🧠 解题思路：前缀和 + 哈希表统计「历史前缀和」

目标：统计有多少个区间 [i, j] 满足
$$
\text{sum}(i, j) = k
$$
设 pre[x] 为下标 0..x 的前缀和，则有：
$$
\text{sum}(i, j) = pre[j] - pre[i-1]
$$
想要 sum(i, j) == k，等价于：
$$
pre[j] - pre[i-1] = k \Rightarrow pre[i-1] = pre[j] - k
$$
这句话的意思是：

当前前缀和为 pre 时，只要之前有多少个前缀和等于 pre - k，
就有多少个子数组以当前下标结尾、和为 k。

核心做法

用一个变量 pre 维护当前前缀和；
用一个哈希表 cnt 维护「前缀和数值 → 出现次数」；
遍历数组：
- 每来一个数 x，更新 pre += x
- 查询之前有多少个前缀和等于 pre - k，把这个次数加进答案
- 然后把当前前缀和 pre 计入 cnt 中

关键细节：为什么 `cnt` 初始为 `{0: 1}`？

对于从下标 0 开始的子数组 [0..j]：
- 其和为 k 的条件是：pre[j] == k
- 对应公式 pre[j] - pre[-1] = k，可以把 pre[-1] 视为 0
所以一开始就认为「前缀和为 0」出现过一次，代表「什么都没选」。

👉 一句话总结：
遍历过程中每次看「历史上有多少个前缀和 == 当前前缀和 - k」，这些都可以和当前前缀和配成一个和为 k 的子数组。

⚠ 为啥不用滑动窗口？
因为有负数，窗口和在扩张或收缩时不单调，没法只靠左右指针贪心推进。

✅ Python 代码（类方法版）

from typing import List

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        pre = 0                  # 当前前缀和
        cnt = {0: 1}             # 前缀和 -> 出现次数，初始有一个前缀和为 0
        res = 0                  # 结果：子数组个数

        for x in nums:
            pre += x

            # 查找：之前有多少个前缀和 = pre - k
            need = pre - k
            if need in cnt:
                res += cnt[need]

            # 记录当前前缀和
            cnt[pre] = cnt.get(pre, 0) + 1

        return res

🪄 核心逻辑表

遍历位置	当前值 `x`	当前前缀和 `pre`	需要的前缀和 `need = pre - k`	贡献个数	更新 `cnt[pre]`
第 i 个	`nums[i]`	`pre += x`	在哈希表中查询	`+cnt[need]`	`cnt[pre] += 1`

cnt[need] 的含义：
历史上有多少个位置 t，使得 pre[t] == pre[i] - k，
这些 t+1..i 都是和为 k 的子数组。

⏳ 复杂度分析

时间复杂度：O(N)
单次遍历，每步哈希表查询与更新均为均摊 O(1)。
空间复杂度：O(N)
最坏情况下，每个前缀和都不同，哈希表存 N 个键。

🧷 小结口诀

前缀一路往前累，
哈希记录来时轨。
当前减去目标 k，
历史匹配全作对。

✅ 关键词记忆：前缀和、哈希表统计频次、pre - k、cnt = {0: 1}

滑动窗口总结

一、滑动窗口本质是什么？

一句话：

在连续区间上做文章，用两个指针维护一个“动态子数组 / 子串”，在移动过程中维持某种性质或统计量。

区别点：

必须是连续的：子数组 / 子串，而不是子序列。
关注的是：区间长度 / 区间和 / 区间内种类数 / 频率 / 最大最小值之类的东西。
解法需要在 O(N) 或 O(N log N) 内完成。

形式上几乎都是：

left = 0
for right in range(n):
    # 扩大窗口，把 nums[right] / s[right] 加进来
    ...

    while 不满足条件:
        # 缩小窗口，把 nums[left] / s[left] 移出去
        left += 1

    # 此时窗口满足某种条件，可以在这里更新答案

二、什么题适合用滑动窗口？怎么一眼识别？

你可以当成一道“读题匹配模板”的选择题，看下面这些特征出现了几个：

1. 关键词特征

如果题目里出现这些描述，窗口警报直接拉响：

“子数组 / 子串” + “连续”
“最长 / 最短的满足某性质的子数组 / 子串”
“统计满足某条件的子数组数量”
“所有长度为 k 的子数组 / 子串的 xxx”
“区间内至多 / 不超过 / 至少 / 恰好 k 个 xxx”

典型关键词组合：

最长 + 子串 + 不含重复字符
最小 + 覆盖子串
所有长度为 k 的子数组的和 / 均值 / 最大值
子数组积 < k，子数组和 <= k
至多 k 个不同字符、至多 k 次替换

2. 数据范围特征

n 在 1e5 ~ 1e6 这种量级
→ 明示你别想 O(N^2)，要 O(N) 模式。
元素是整数 / 字符，结构简单，不是花里胡哨的树 / 图

3. 题目行为特征

问题本质是：

“在一条线段上刷一个区间，这个区间要一边往右滑，一边根据条件收缩左边界。”

如果你发现可以只往右遍历一遍数组，每个元素进窗口一次、出窗口一次，那就非常滑动窗口味。

三、滑动窗口的常见题型分类

1. 固定长度窗口（最简单那一挂）

特征：

明确写了「长度为 k 的子数组 / 子串」
问题只在固定长度窗口上做统计
比如：最大和、平均值、包含某种模式次数等

套路：

先求前 k 个的结果
然后每次右指针右移一格，左边扔一个，右边加一个，O(1) 更新

典型题：

长度为 k 的子数组的最大和
所有长度为 k 的子串中包含多少个某字符

2. 可变长度窗口（经典模板）

这是你最近刷得最多的一类。

特征：

没给固定长度，而是说
- 「最长子串满足 xxx」
- 「最短子串满足 xxx」
- 「子数组和 ≤ k / < k」
- 「至多 k 个不同字符」
条件一般是“区间内某种统计量必须满足一个约束”。

套路：

right 一直往右走，把元素丢进窗口；
每进一个元素，就看当前窗口是否违背条件：
- 若违背，就挪 left，把左边的元素往外扔，直到重新满足条件；
每次窗口合法时，就可以：
- 更新答案（长度、数量）
- 或者用窗口状态做统计

例子：

最长无重复字符子串
窗口内字符不能重复，用 map[char] -> 次数 维护，超过 1 了就收缩左边。
找到字符串中所有字母异位词（长度固定 + 频次匹配）
乘积小于 K 的子数组
所有元素正数，用乘积和除法配合滑动窗口。

3. 计数型：`至多 K / 恰好 K` 模式

文本题里的高频模式。

特征：

至多 K 个不同字符 / 1 的个数 / 替换次数
恰好 K 次 / K 个不同元素

核心技巧：

恰好 K = 至多 K - 至多 (K-1)

例子：

子数组中恰好 K 个不同整数的个数
子串中恰好 K 种不同字符的个数

代码会有两个窗口函数：atMost(K) 和 atMost(K-1)。

4. 区间最值型窗口：单调队列

这类属于滑动窗口的进阶分支。

特征：

题目明确要求「每个窗口的最大值 / 最小值」
窗口长度给定，一般就是 [i, i+k-1] 每个都要一个最值
暴力每次 O(k) 求最值会超时

套路：

用单调队列（双端队列）维护一个「候选最大值下标」
队列头永远是当前窗口最大值下标
窗口右移：
- 把新元素从队尾不断比较，小的都弹掉
- 再把新元素下标加进去
- 同时检查队头是否已经滑出窗口，滑出了就弹掉

典型题：

滑动窗口最大值
每个长度为 k 的窗口的最小值

5. “伪窗口”：前缀和 + 双指针混合型

有些题你以为是滑动窗口，其实标准解是前缀和 + 哈希表，比如刚才的：

560. 和为 K 的子数组

这题之所以不能用经典滑动窗口，是因为有负数，区间和不单调。

但有些“全是非负数”的版本：

子数组和 ≤ K 的最长长度
子数组和 == K 的个数（所有元素非负）

这时候就能用真·滑动窗口了。
识别方式：题目明确说“非负”或“数组只包含正整数”，你就可以开始贪心扩 + 缩。

四、滑动窗口的核心思路（终极模板）

把所有题抽象一下，滑动窗口其实就两个动作：

right 不断右移，尝试扩大窗口（加入新元素）
当窗口不合法时，用 left 收缩窗口，恢复合法

伪码统一长这样：

left = 0
for right in range(n):
    # 1. 扩大窗口，纳入 nums[right]
    add(nums[right])

    # 2. 如果当前窗口不满足题目要求，就缩小
    while 不合法:
        remove(nums[left])
        left += 1

    # 3. 此时窗口是合法状态，可以用来更新答案
    update_answer(left, right)

核心在于：

你要精确定义 “合法 / 不合法” 是什么；
知道怎么在 add 和 remove 里维护状态，例如：
- 当前窗口字符计数
- 当前窗口中「不同元素个数」
- 当前窗口和 / 积 / 最大值 / 最小值
- 目前违反条件的元素数量

五、难点 & 突破点

难点 1：什么时候该缩？条件怎么写？

很多人窗口写崩就是因为这一行：

1	while 不合法:

写成一会儿死循环，一会儿少算。

突破点：

明确区分这两类题：
1. “至多型”条件：
  - 例如「至多 K 个不同字符」，你要在 cnt_distinct > K 时缩。
2. “至少型 / 覆盖型”条件：
  - 例如「包含所有字符」、「和 ≥ K」，在 满足条件时可以缩 来找最短。
习惯性问自己：
- 题目要的是最长还是最短？
- 你希望窗口「刚刚好合法」时再更新答案吗？

难点 2：`left` / `right` 的边界 & 索引

常见翻车点：

窗口长度是 right - left + 1 还是 right - left？
记录答案的时候用的是 left 还是 left+1？
固定长度窗口里，left = right - k 这一类下标关系。

解决方式很无聊：
手动带一个小样例干一遍，确认每次窗口实际覆盖的范围。
比如：

s = "abcd", k = 3
right = 2 时，窗口是 [0, 2]，长度 = 3
right = 3 时，left = right - k = 0 → [0, 3] 长度 4
但如果你要固定长度 3，就必须先减再加：
left = right - k
窗口是 [left+1, right] = [1, 3]

难点 3：多条件 / 多维状态

问题一复杂，就会出现这种事情：

窗口里既要控制「不同字符数」，
又要控制「总长度」，
还要匹配「字符串频次关系」。

比如：

最小覆盖子串（Minimum Window Substring）
需要用两个 map：目标频次 + 当前窗口频次，一堆条件交织。

突破点：

明确一个「窗口合法的判定条件」，写成一个可以检查的逻辑：
- 比如：valid_count == len(need)
  表示所有需要的字符都满足了频次；
扩张时让窗口从「不合法 → 合法」，收缩时保证「不从合法变回不合法」之前及时更新答案。

难点 4：什么时候滑动窗口会假冒题解？

像你刚抓住的点：
有负数 + 要求子数组和 = k，结果被标签挂了个 Sliding Window。

识别思路：

如果你需要精确等于某个和值，而且数组里有负数
→ 一般要想到前缀和 / 哈希，不要硬滑窗。
滑动窗口的本质是：你通过左右移动可以“有方向地改变窗口性质”（单调变好或变坏）。
一旦这个方向性消失（比如和因为负数乱跳），就别勉强它是窗口题。

六、最后给你一个「滑动窗口识别 Checklist」

读题时可以在心里默念：

问的是子数组 / 子串，而且要求连续吗？
关注的是一个区间性质 / 统计量吗？
- 长度 / 个数 / 种类数 / 和 / 积 / 最大最小值…
想要的答案是：
- “最长 / 最短满足条件的子数组”？
- “满足条件的子数组数量”？
- “每个窗口的某个统计值（固定长度）”？
题目数据量大到不能 O(N^2)？
数组是否全非负？
- 若要搞区间和 / 积，并且全非负，很适合窗口。
临时状态能在「元素进 / 出窗口」时用 O(1) 更新吗？

满足 3~4 条，就可以第一时间往滑动窗口靠。
不满足的，才去考虑前缀和、单调栈、DP 那些亲戚。

标题: LeetCode笔记
作者: Serendy
创建于 : 2025-12-02 13:37:19
更新于 : 2025-12-11 20:42:53
链接: https://mapleqian.github.io/49036.html
版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。

#Note

LeetCode笔记

Python数据结构

0. 总体地图：都有哪些东西？

1. list：动态数组（Python 亲儿子）

1.1 创建

1.2 访问 & 切片

1.3 修改

1.4 删除

1.5 其他常用

2. tuple：不可变的“只读 list”

2.1 创建

2.2 用途

3. str：不可变字符串

3.1 常用操作

4. dict：哈希表（键值映射）

4.1 创建

4.2 插入 / 修改

4.3 访问

4.4 遍历

4.5 删除

5. set：去重 + 成员判断神器

5.1 创建

5.2 常用操作

5.3 集合运算

6. collections 里常见几位

6.1 deque：双端队列

6.2 defaultdict：带默认值的 dict

6.3 Counter：频数统计

6.4 namedtuple：轻量级“结构体”

7. heapq：最小堆（优先队列）

8. 一个简单小总表（当速查用）

哈希表

散列（哈希）函数的构造方法

1 直接定址法

2 除留余数法

3 数字分析法

4 折叠法

5 平方取中法

6 随机数法

冲突处理方法

1 开放定址法

1 线性探测法 P130

2 平方探测法 P132

3 双散列探测法 P133

2 再哈希法

3 链地址法

4 建立一个公共溢出区

算法实现

性能分析

🎯 两数之和（Two Sum）

🧩 题目描述

📌 示例

示例 1

示例 2

示例 3

🧠 解题思路：哈希表，边走边找对象

✅ Python 代码（哈希一遍扫描）

🧩 核心逻辑表

⏳ 复杂度分析

🪄 小结口诀

🔤 字母异位词分组（Group Anagrams）

🧩 题目描述

📌 示例

示例 1

示例 2

示例 3

🧠 解题思路：给每个单词“做指纹”，用哈希表分组

思路一：排序当“签名”（最常用、好写）

思路二：26 维频次数组当“签名”（更偏底层一点）

✅ Python 代码：排序版（推荐，先写这个）

✅ Python 代码：计数版（进阶一点）

🧩 核心逻辑表

⏳ 复杂度分析

排序版

计数版

🪄 小结口诀

补充：本题哈希表底层原理

1️⃣ 整体结构长啥样？

2️⃣ 具体走一遍插入过程

第一步：插 "eat"

6.1 `deque`：双端队列

6.2 `defaultdict`：带默认值的 dict

6.3 `Counter`：频数统计

6.4 `namedtuple`：轻量级“结构体”

第一步：插 `"eat"`

第二步：插 `"tea"`

第三步：插 `"tan"`

插入（`mp[key].append(x)`）脑内流程：

查询（`key in mp` 或 `mp[key]`）脑内流程：